网站首页 行业快讯 > 正文
反三角函数定义域(三角函数和反三角函数的之间的关系和定义域)
大家好,我是专升本数学学霸,这次我们继续来讨论三角函数和反三角函数的之间的关系和定义域。那你知道有哪些三角函数和反三角函数以及它们之间的关系和定义域吗?学霸来帮你来了。
首先,我们来看看有哪些三角函数,正弦函数sin α, 余弦函数cos α,正切函数 tan α,余切函数cot α,正割函数sec α,余割函数csc α。
接下来,我们来看看有哪些反三角函数,反正弦函数arcsin α,反余弦函数 arccos α,反正切函数arctan α,反正割函数 arcsec α, 反余割函数 arccsc α。
继续。我们来看看它们之间的关系。
反三角函数和三角函数互为反函数。一般来说,设函数y=f(x)(x∈A)的值域是C,若找得到一个函数g(y)在每一处g(y)都等于x,这样的函数x= g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数,记作x=f-1(y) 。反函数x=f -1(y)的定义域是函数y=f(x)的值域,反函数x=f -1(y)的值域是函数y=f(x)的定义域。正函数与反函数的图像是关于y=x对称,最具有代表性的互为反函数就是对数函数与指数函数。有关反函数的内容下次具体讨论。三角函数的之间关系:三角形函数的关系可以用六边形表示,如图1所示。
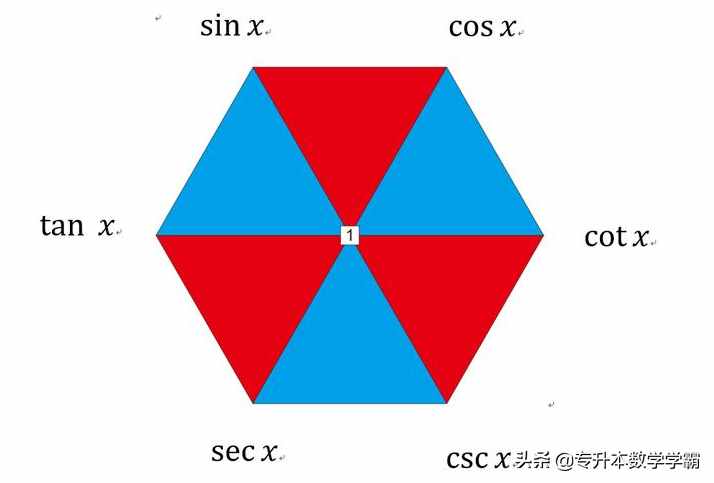
图1 三角函数的六边形法则
①平方关系,在六边形中,红色区域的倒三角形成平方关系。
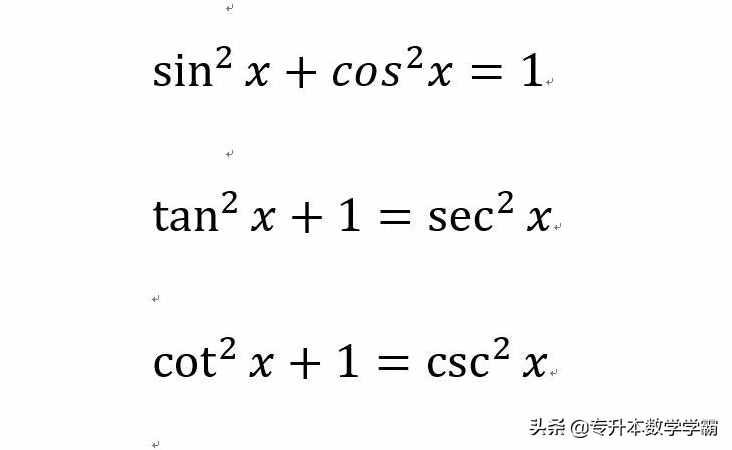
图2 平方关系
②比值关系,在六边形中,任意一点的值是前面相邻两个函数的比值。
图3 比值关系
③倒数关系,在六边形中,六边形的对角线的两个三角函数成倒数关系。
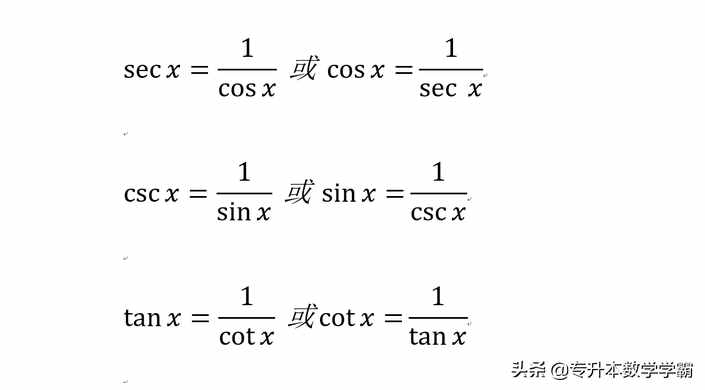
图4 倒数关系
④ 乘积关系,在六边形中 任意一点的值等于紧挨着这一点的两个端点值 的积
图5 乘积关系
三角函数的定义域:
我们一起分别来讨论它们的定义域和值域:
①正弦函数sin α的定义域是一切实数R,值域是[-1,1],其函数图象如图6所示:
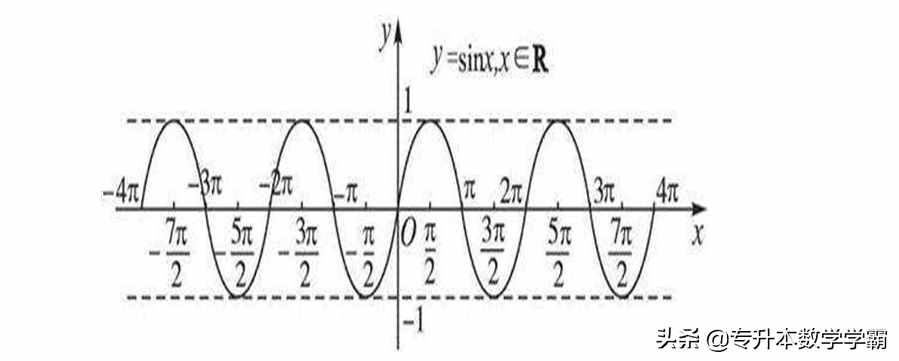
图6 正弦函数图像
由图象可知,正弦函数是奇函数,周期 T=2π,其对称性是关于原点对称,单调性:单调递增区间:[-π/2±2kπ,π/2±2kπ] ,(K∈Z) ;单调递减区间:[π/2±2kπ,3π/2±2kπ],(K∈Z)。正弦函数的定义域是反正弦函数的值域,正弦函数的值域是反正弦函数的定义域。
②余弦函数cos α的定义域是一切实数R,值域是[-1,1],其函数图象如图7所示:
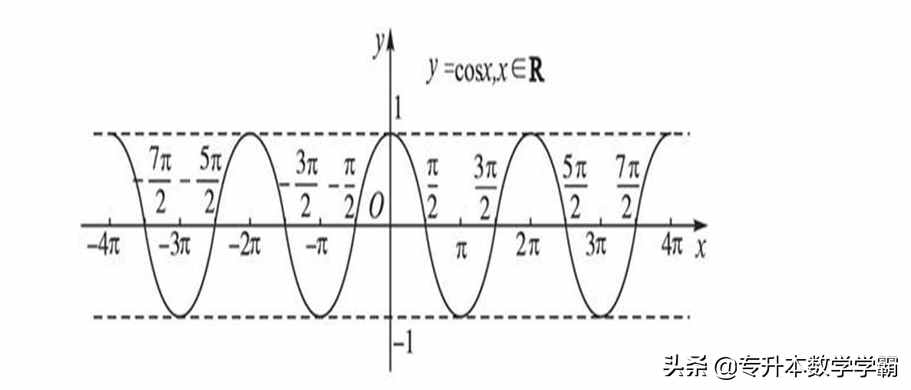
图7 余弦函数图像
由图象可知,余弦函数是偶函数,周期 T=2π,其对称性是关于y轴对称,单调性:单调递增区间:[π±2kπ,2π±2kπ] ,(K∈Z) 单调递减区间:[0±2kπ,π±2kπ],(K∈Z)。余弦函数的定义域是反余弦函数的值域,余弦函数的值域是反余弦函数的定义域。
③正切函数 tan α的定义域是α ≠ π/2+kπ,(K∈Z),值域是一切实数R,其函数图像如图8所示:
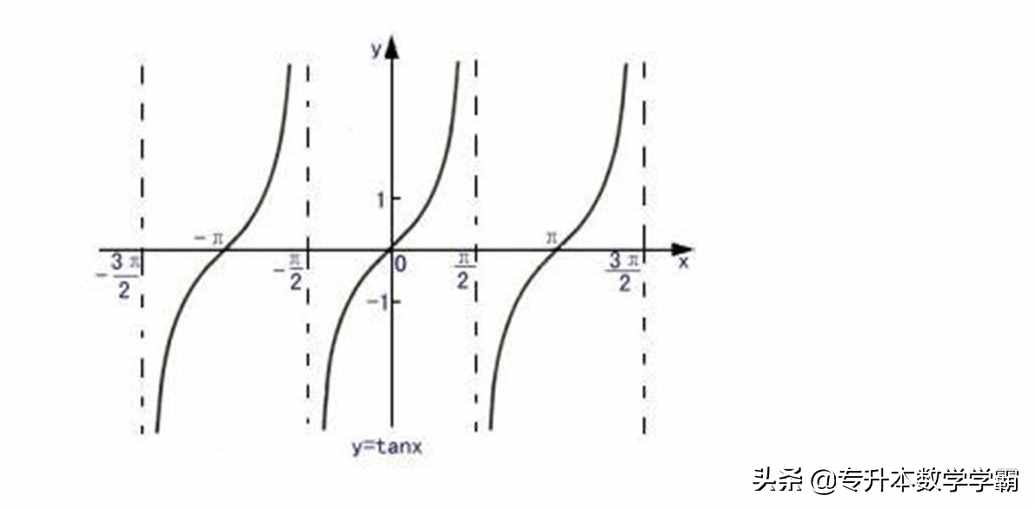
图8 正切函数图像
由图象可知,正切函数是奇函数,周期 T=π,其对称性是关于原点对称,单调性只有单调递增,单调递增区间为[-π/2±kπ,π/2±kπ] ,(K∈Z),没有单调递减。正切函数的定义域是反正切函数的值域,正切函数的值域是反正切函数的定义域。
④ 余切函数cot α的定义域是 α≠kπ,(K∈Z) 值域是一切实数R,其函数图象如图9所示:
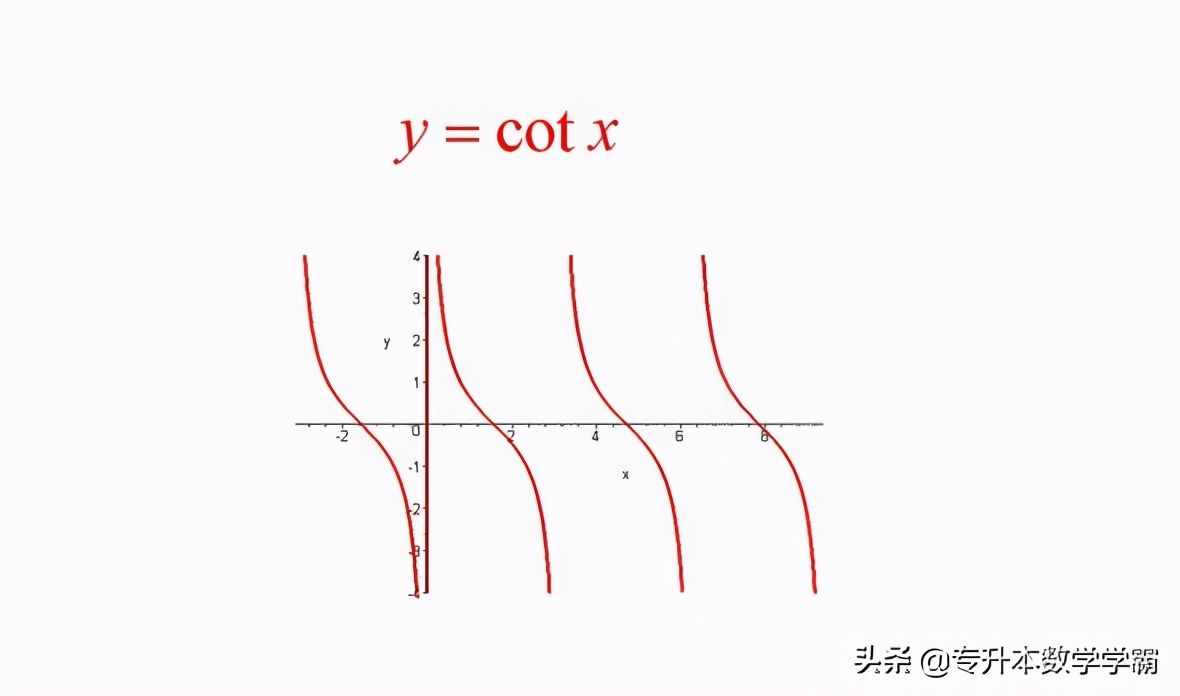
图9 余切函数图像
由图像可知,余切函数是奇函数,周期 T=π,其对称性是关于原点对称,单调性只有单调递减,单调递减区间为[0±kπ,π±kπ] ,没有单调递增。余切函数的定义域是反余切函数的值域,余切函数的值域是反余切函数的定义域。
由于正割函数sec α、余割函数csc α、反正割函数arcsec α、反余割函数arccsc α,专升本数学不考,加上正割函数、余割函数、反正割函数、反余割函数的图像麻烦,就不进行研究了。
今天的讨论到此为止,以上内容是我个人见解,不代表官方的意见,下次我们来讨论其他函数的五种性质:单调性、奇偶性、对称性、周期性、有界无界性。
版权说明: 本文由用户上传,如有侵权请联系删除!
猜你喜欢:
- 2022-09-20 男人恶心是什么病的前兆(恶心是什么病的前兆)
- 2022-09-20 山东财经大学东方学院考研率怎么样(山东财经大学考研率是多少)
- 2022-09-20 广西最早的大学叫什么大学(在桂林设立的广西最早的大学是哪所大学)
- 2022-09-20 小儿肺炎有5个常见症状吗(小儿肺炎有5个常见症状)
- 2022-09-20 m是哪个服装品牌的标志(标志为M的衣服是什么牌子的)
- 2022-09-20 什么叫正比例什么叫反比例举例说明(什么叫反比例,举个例子说明,)
- 2022-09-20 一包烟要多少根烟丝(一包烟要多少根)
- 2022-09-20 男人吃樱桃对身体有什么好处(男人吃樱桃有什么好处)
最新文章:
- 2023-07-02 怎样挑选新鲜的猪肝?(怎么挑选新鲜猪肝 挑选新鲜猪肝的小技巧)
- 2023-07-02 木地板都有哪些种类(木地板的种类有哪些)
- 2023-07-02 白蜡木家具的优缺点(松木家具的优缺点)
- 2023-07-02 怎么清洗窗帘布上的污垢(怎么清洗窗帘)
- 2023-07-02 世界上最可爱的小仓鼠的样子(可爱小仓鼠的种类)
- 2023-07-02 小猫拉不出来屎怎么办(小猫拉不出屎怎么办)
- 2023-07-02 新飞小冰箱耗电量一天多少度(小冰箱耗电量一天多少度)
- 2023-07-02 公司注销工业房产怎么办手续(公司注销工业房产怎么办)
- 2023-07-02 凤凰层到底好还是不好(凤凰层是哪一层)
- 2023-07-02 马桶宽度空间留多少(马桶两边的空间大小是多少)
- 2023-07-02 如何训练猫咪小便(如何训练猫大小便)
- 2023-07-02 卫生间吊顶防潮层做法图集(卫生间吊顶方法是什么)
- 2023-07-02 狗狗为什么总是流口水怎么办(狗狗为什么爱流口水)
- 2023-07-02 卧室窗户漏水由谁负责维修(卧室窗户漏风怎么办)
- 2023-07-02 世界名猫大全(世界名猫你知道几种)
- 2023-07-02 applewatchseries7和6对比(apple watch series 7和6的区别)
